The Collatz Conjecture was proposed by mathematician Lothar Collatz in 1937 and remains unsolved to this day. It states that regardless of the starting number (belonging to the natural numbers), it will always reach 1, and thus form a cycle of 4-2-1.
The function is given by:
| n/2 , if n is even
f(n) = | ∀ n ∈ ℕ
| 3n+1 , if n is odd
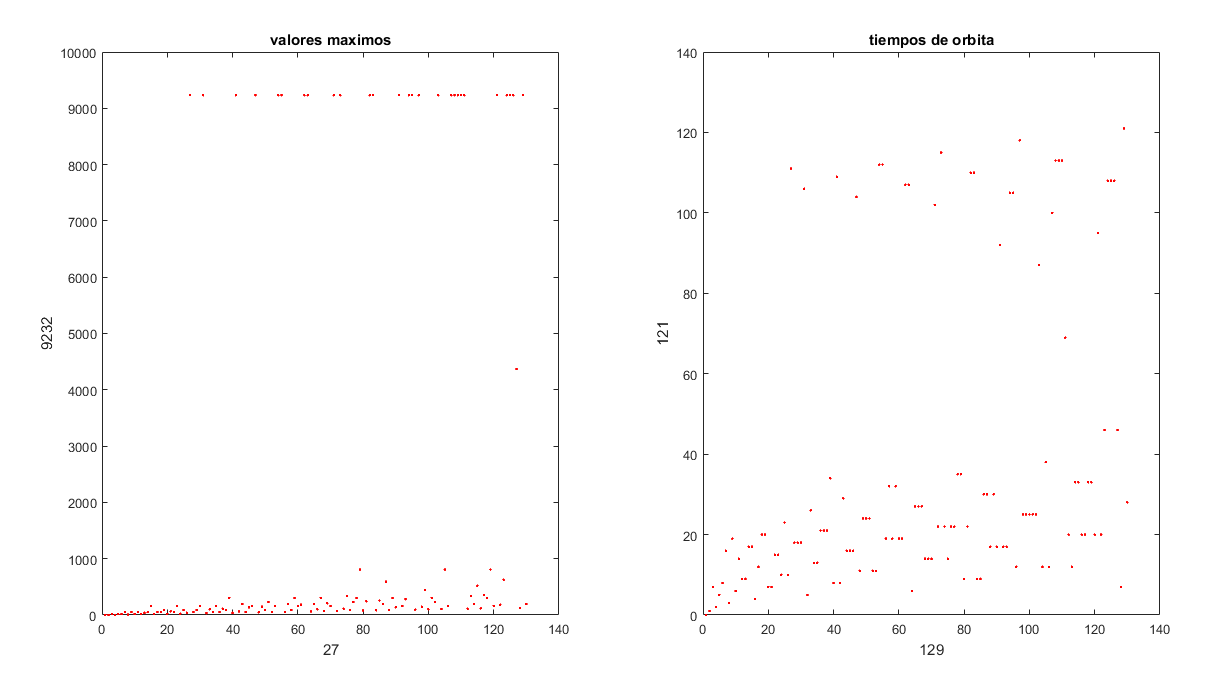
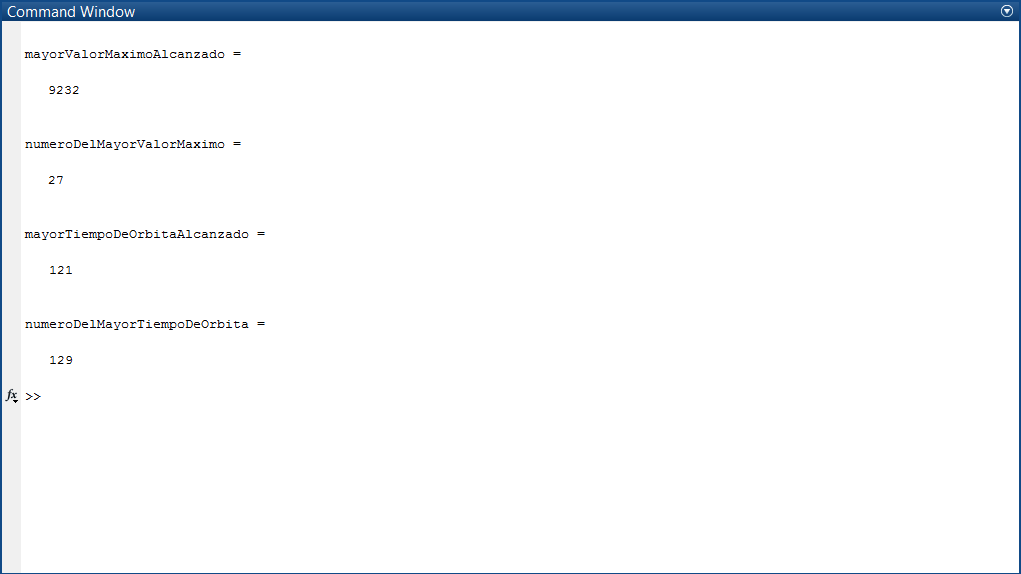
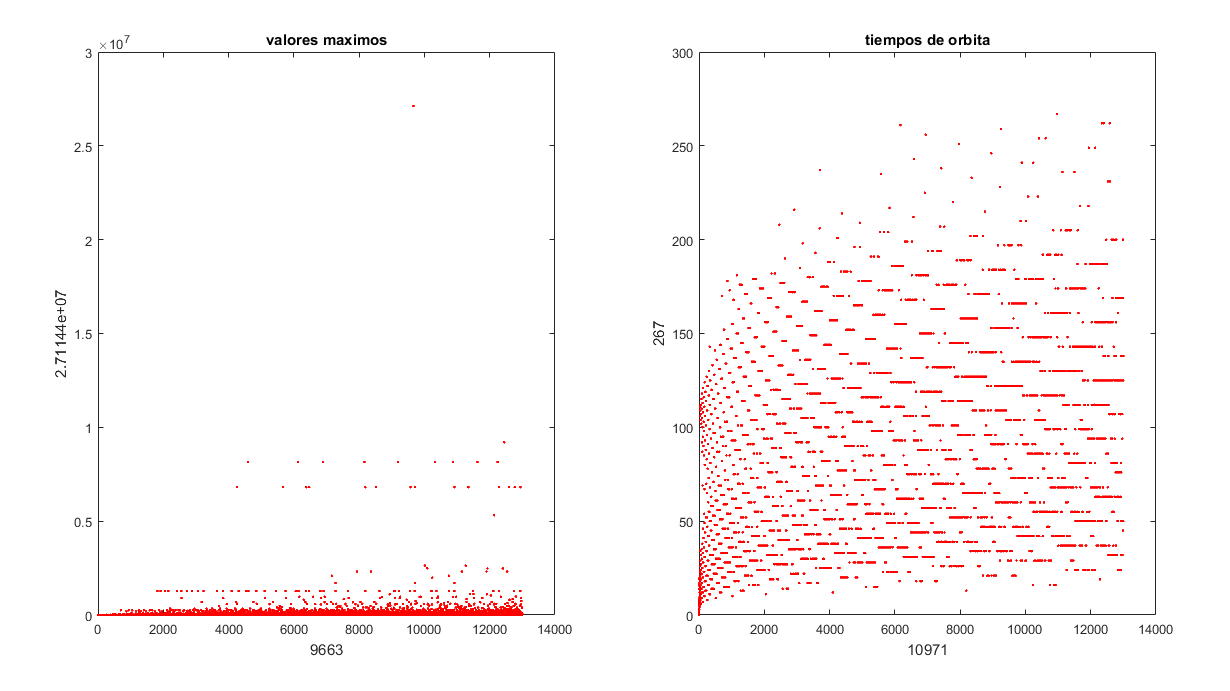
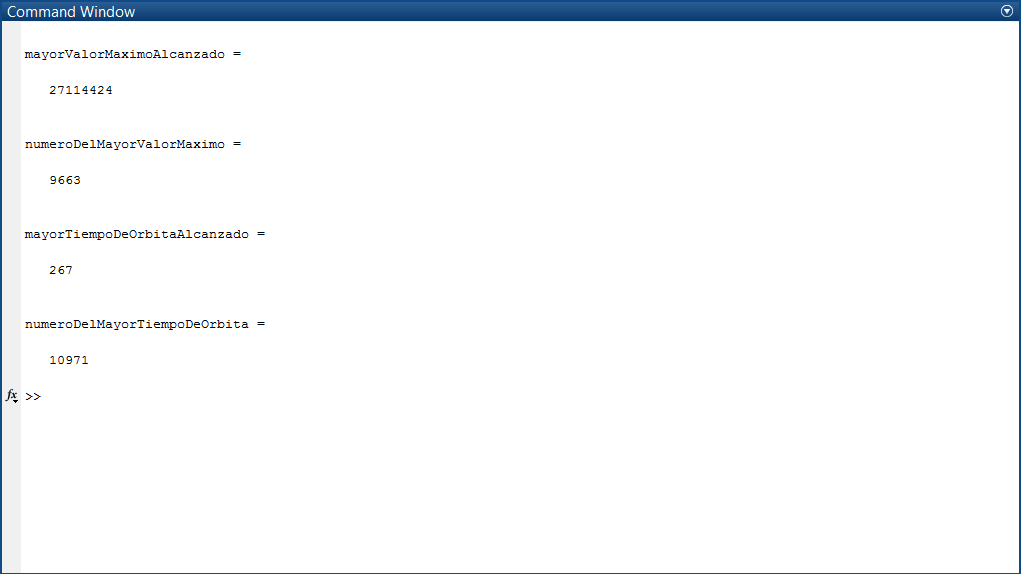
The most important data to consider when executing the function with a given number are the orbit time, which refers to the number of iterations until reaching 1, and the upper bound, which is the highest value obtained during the iterations.
Although neither the truth nor falsehood of the conjecture has been proven, in May 2020, the conjecture was verified for all sequences of numbers less than 2^68.
On my part, I wanted to create a small C program capable of accepting any number, performing the iterations, and returning the orbit time and the maximum value reached. Then, seeking to graph the results and compare them, I moved to MATLAB and modified the code to iterate through all numbers less than the one entered by the user, graphing the orbit time and the maximum values reached; finally displaying the largest of the maximum values and the longest orbit time obtained, along with their respective initial values.
Below are 3 examples performed with n equal to 130, 1300, and 13000. If you are interested in downloading the code, it is available at link.