Casino games!

I don't know about you, but I have always looked for a way to beat the casino. But how?

First, let's analyze how a casino operates, what games most casinos have, at least in Argentina, and which ones we should play to maximize our profits.

A casino is an establishment where the main attraction is games of chance. The logic of all these games, at its most basic level, involves a player making a bet in one of the games, where, if the winning condition is met, the player is returned an amount equal to or greater than their bet, or otherwise, the player loses their bet.

The winning conditions, bets, and payouts are predetermined. These are determined by statistics to give a certain advantage to the casino. Thus, if we think of a player who plays indefinitely, the balance would tilt in favor of the casino according to the previously stipulated proportion. It is worth noting that these probabilities in electronic games are regulated by a governing body to ensure they are not excessively abusive towards the population, but the lack of periodic controls means that this is not always upheld.

Now, assuming everything works correctly, which game should we play? In casinos, we can find slot machines, roulette, blackjack, dice games, and poker.

We need to analyze how we interact with the game. If our goal is to maximize the probability of winning, we must discard all those games where we cannot decide the value of the bet or how we place it; thus, slot machines are out.

On the other hand, poker, although it involves chance, depends largely on the player's skill, making it the game where a player might have the best odds of winning. However, since this solely depends on the player, a method that replicates results for everyone cannot be obtained, so it is also excluded from this analysis.

Finally, we have roulette, blackjack, and dice games. In these games, in addition to chance, there is player interaction, allowing us to plan a strategy to increase our chances of winning. To determine which of them gives better chances, let's review their rules and calculate the probabilities.

Craps

When playing in a casino against the bank or house, one or more players place various bets on the outcome of the dice thrown by a designated shooter. To start the game, during what is known as the "come-out roll," the player must place a bet known as the "pass line," where they aim to roll a seven (known as a natural seven or winning seven) or an eleven to win the bet, which pays one to one. If they roll a two, three, or twelve (known as craps), they automatically lose their bet and will need to place another bet to continue rolling.

If the first roll does not yield a seven or eleven (which would win) or a two, three, or twelve (which would lose), the game enters a second stage, where the point will be established based on the number rolled (four, five, six, eight, nine, or ten). In this stage, the shooter will aim to roll that point number again before rolling a seven (referred to as "seven out"). If they successfully repeat the point number, the player wins their bet, and the payout will be one to one. Conversely, if a seven appears, the player loses their bet. In both cases, the round ends, and the game begins anew, although if the round ended due to a seven out, a new shooter will be designated among the various players.

Calculating the probabilities of these situations gives a 22.22% chance of winning on the come-out roll and an 11.11% chance of losing. If any other number appears, the game moves to the second stage, where the player must roll the same value obtained to win, and they lose with a seven. The new probabilities will depend on the number obtained earlier, which will be 13.89% for the numbers 6 and 8, 11.11% for the numbers 5 and 9, and 8.33% for the numbers 4 and 10. Therefore, we find ourselves at a disadvantage against the seven, which has a probability of 16.66% of coming up.

Due to the way the game is played, I do not recommend it, as we begin with a 66% chance of moving to the second stage where, in the best-case scenario, the probability of winning is only 14%.

A better option would be if our bet were of the "don't pass" type, which is practically the opposite of what was described above (but with a 12 as the tie number). In this way, we would have a better probability of winning, although it would still be lower than losing.

With all this, I dismiss dice games as a viable long-term strategy for winning.

Blackjack

Blackjack, also known as twenty-one, is a card game played with one or more English decks of 52 cards without jokers. The goal is to sum a value as close to 21 as possible without exceeding it. Each player at the table plays solely against the dealer, attempting to achieve a better hand than the dealer. The dealer is bound by fixed rules that prevent him from making decisions about the game. For example, he must draw a card whenever his total is 16 or less, and he must stand if he totals 17 or more. The numbered cards add their value, face cards add 10, and the Ace can be worth 11 or 1, at the player's choice. In the case of the dealer, Aces are worth 11 as long as he does not exceed 21, and 1 otherwise. The best hand is to achieve 21 with just two cards, which is an Ace plus a card valued at 10. This hand is known as Blackjack or a natural 21. A Blackjack wins over a 21 achieved with more than two cards.

The dealer deals two visible cards to each player, then places his first card face up, making it visible to the other players, while the dealer has a second card face down awaiting his turn. Each player competes solely against the dealer, ignoring the cards held by other players.

Each player has the option to stand and keep any total or request more cards until they reach 21. Reaching 21 with extra cards does not count as blackjack, making that hand inferior to a blackjack with two cards. If the player exceeds 21 by requesting an extra card, they automatically lose the game, and their cards and bet will be taken by the dealer. After all players have taken their cards, the dealer will reveal his second card and draw more cards as necessary until he totals 17 or more to reach 21, at which point he will stand.

Here are the probabilities of busting when asking for an extra card:

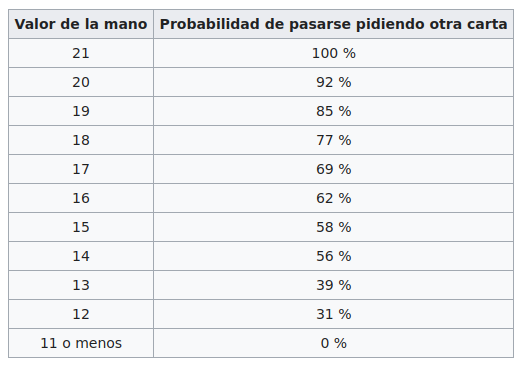
To obtain the exact probabilities for this game requires a more in-depth study due to the numerous variations that can occur, which would take more time than I currently have available. However, broadly speaking, we can state that the dealer has an advantage over the players since they not only compete against him but also against themselves. If they bust over 21, they automatically lose, regardless of what the dealer has. Nonetheless, there are techniques to increase the probability of winning, but they are not well received if discovered.

Roulette

The design currently used in casino roulettes is attributed to the French philosopher and mathematician Blaise Pascal, who sought to create a game where chance was as equitable as possible.

In this design, the arrangement follows these rules:

These rules apply in European roulette (with a single zero) but not in American roulette (with a double zero), where the distribution is more irregular.

Depending on the type of bet, the following payouts can be made:

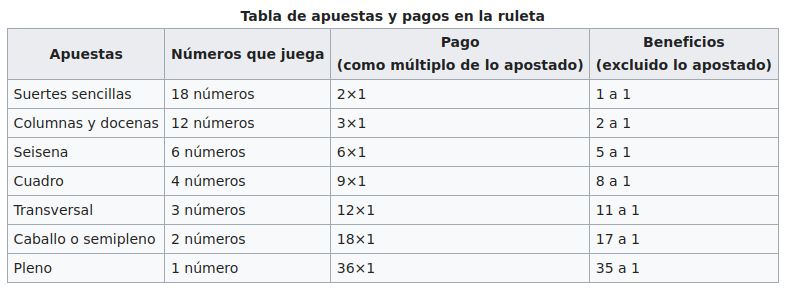
The probabilities of winning are (considering the worst-case scenario with the American version):

For the analysis, we will use the Martingale betting method. This method consists of sticking with even money bets, choosing a category (for this example, I will take red) and maintaining that until we win. This method is based on the premise that if black comes up, the probability of it coming up again is lower, and if it comes up again, the next time it will be even lower, and so on, until red comes up. It is essential to start with the minimum bet, and each time you lose, you must double your bet. When you win, you restart the cycle with the minimum bet. But how effective is it?

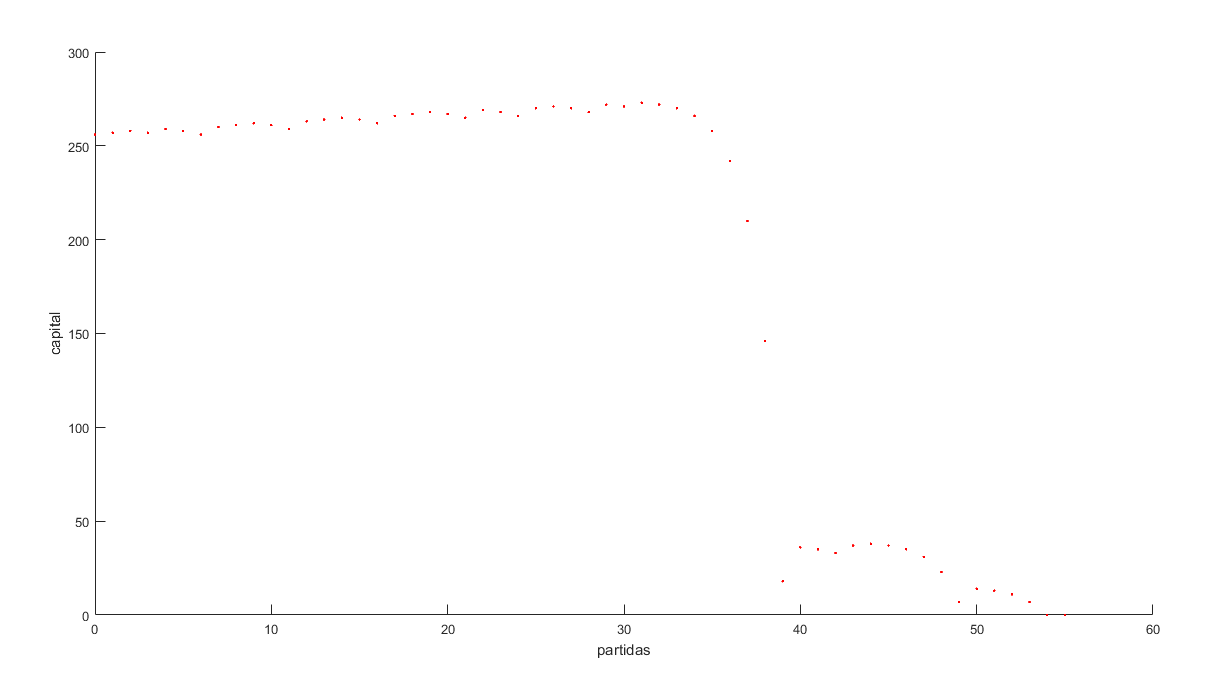
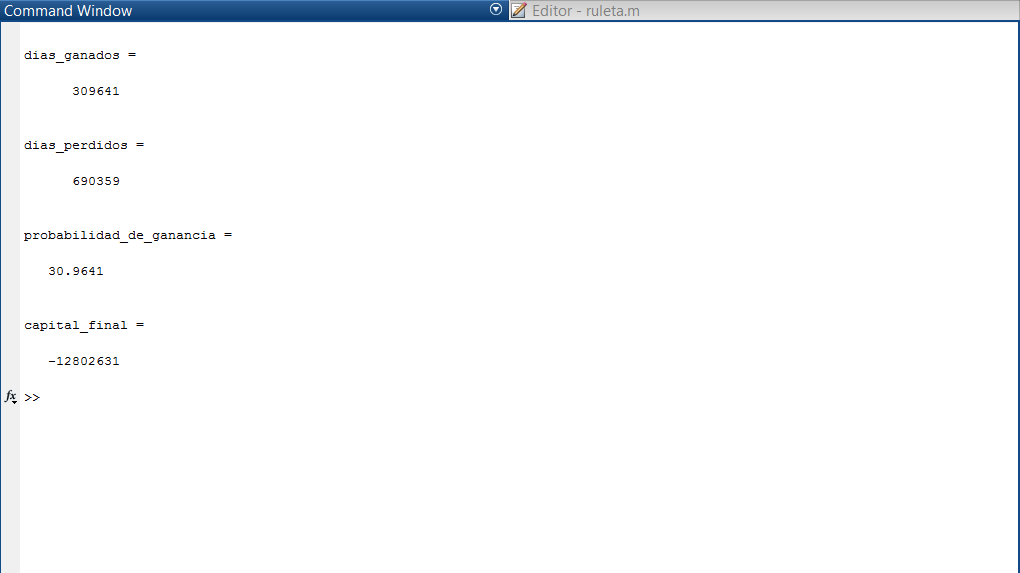
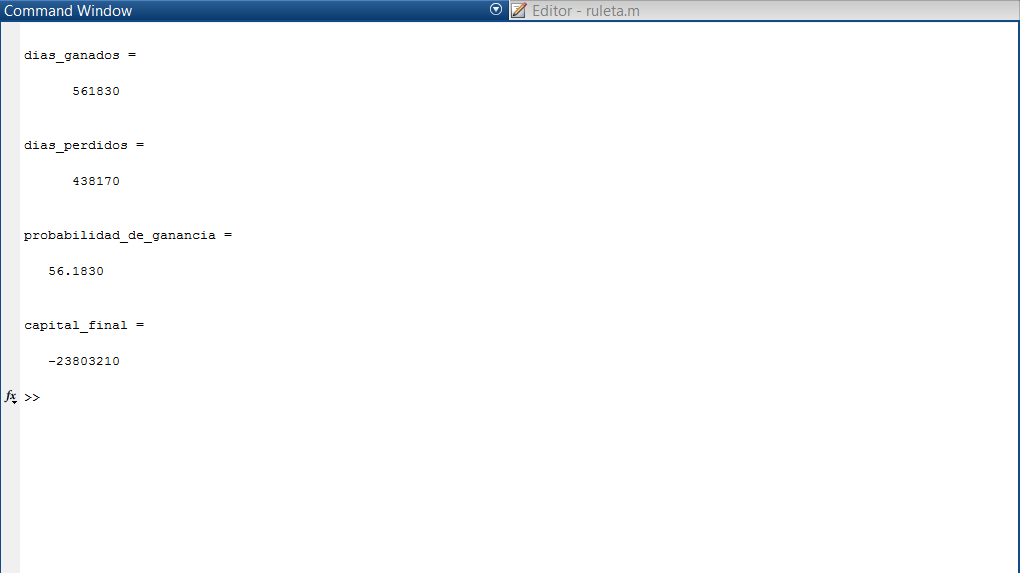
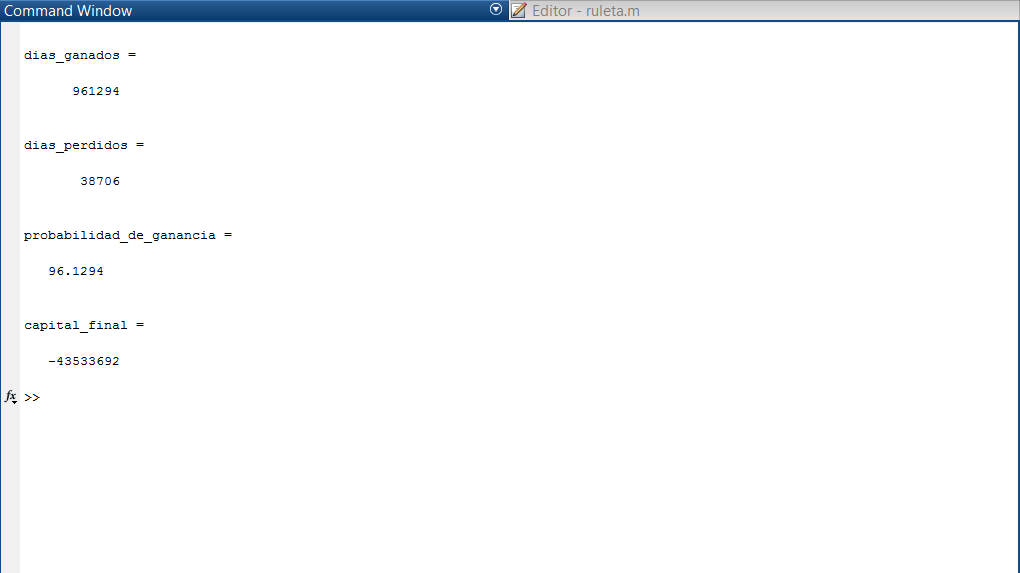
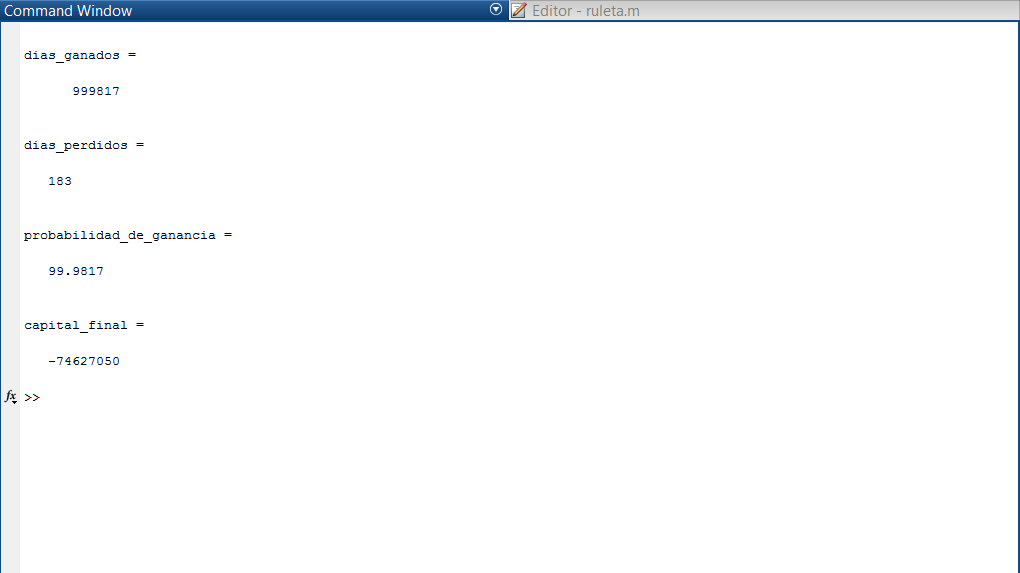
Well, conducting a thorough analysis with MATLAB, I found that the probability is closely related to the minimum and maximum bets allowed by the table, as this determines how many times we can double our bet each time we lose. Based on the data I gathered regarding the minimum and maximum bets generally permitted by casinos, we can double our bet between 6 and 8 times. If we consider that the probability of losing 8 times in a row while maintaining the same color is 0.5%, it’s easy to be tempted to think that the system is infallible, but nothing could be further from the truth.

Through the mathematical model, I discovered that even without betting limitations, and therefore no limitations on the number of times we could double it, the ability to generate long-term profits is null.

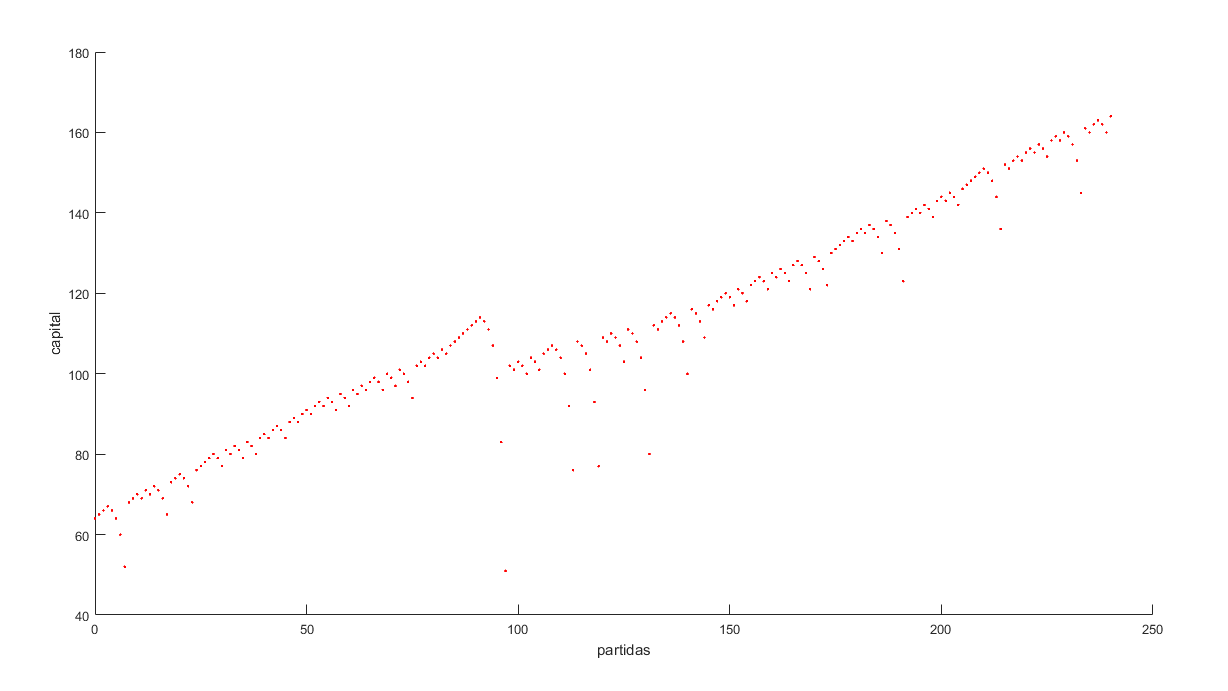
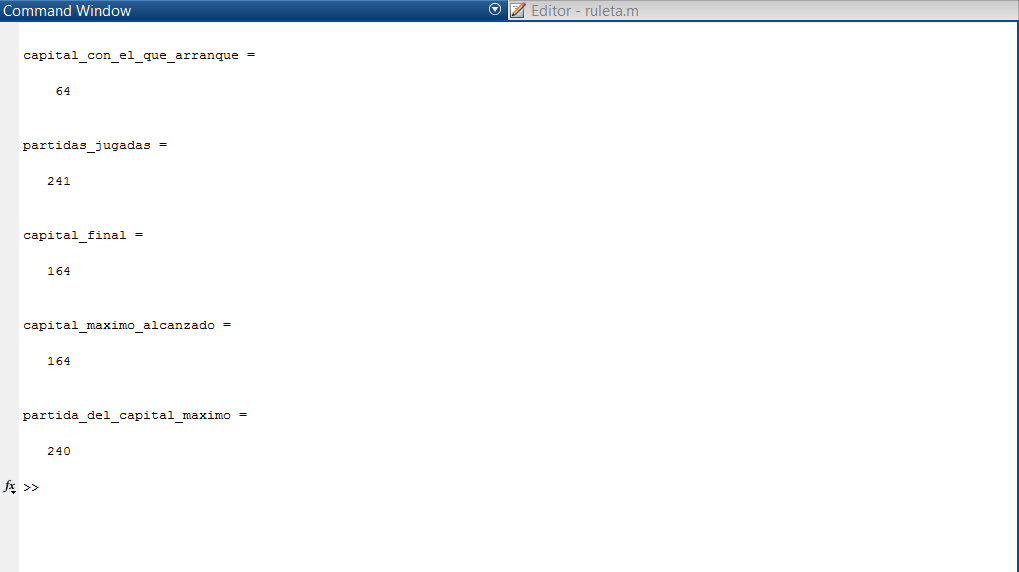
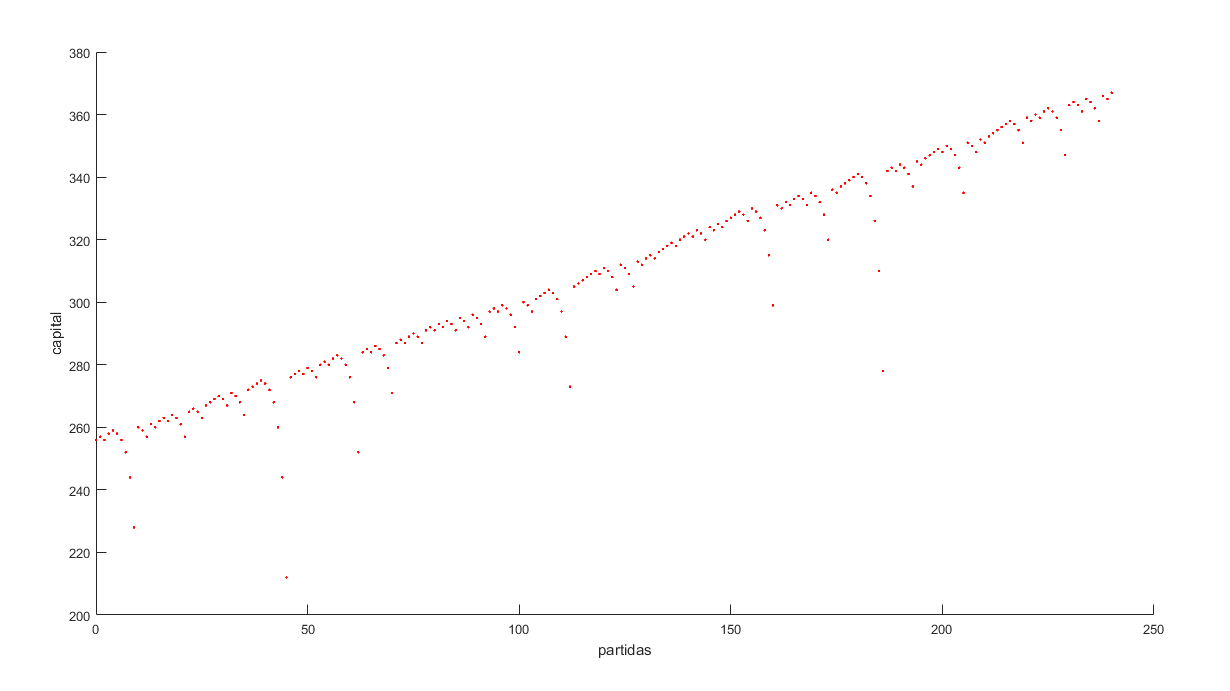
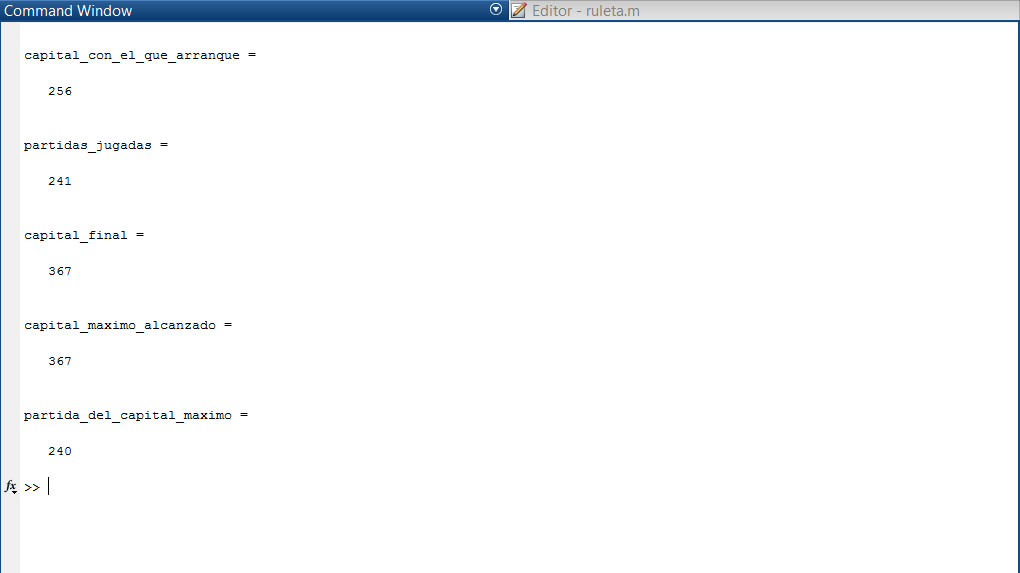
Simulating that I bet 240 times a day (once every 2 minutes over 8 hours) for 1,000,000 days, the probability of winning was around 31%, which means the initial assumption using the Martingale method falls apart since, in the long run, we end up losing 7 out of 10 games.

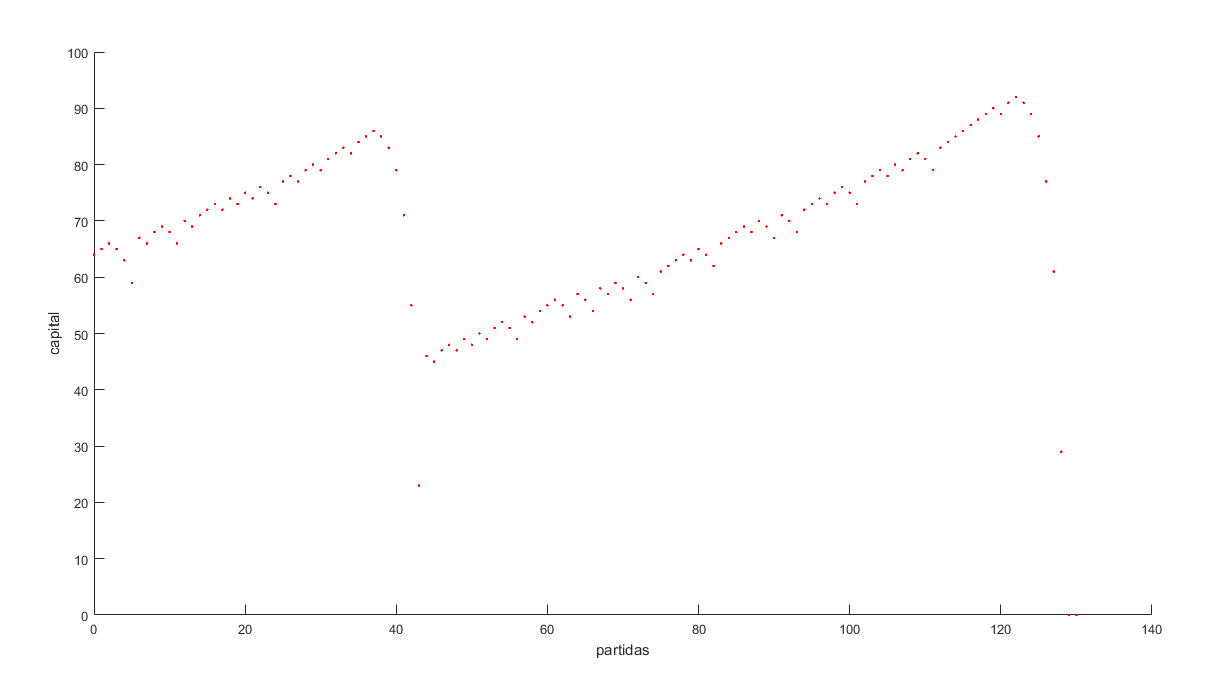
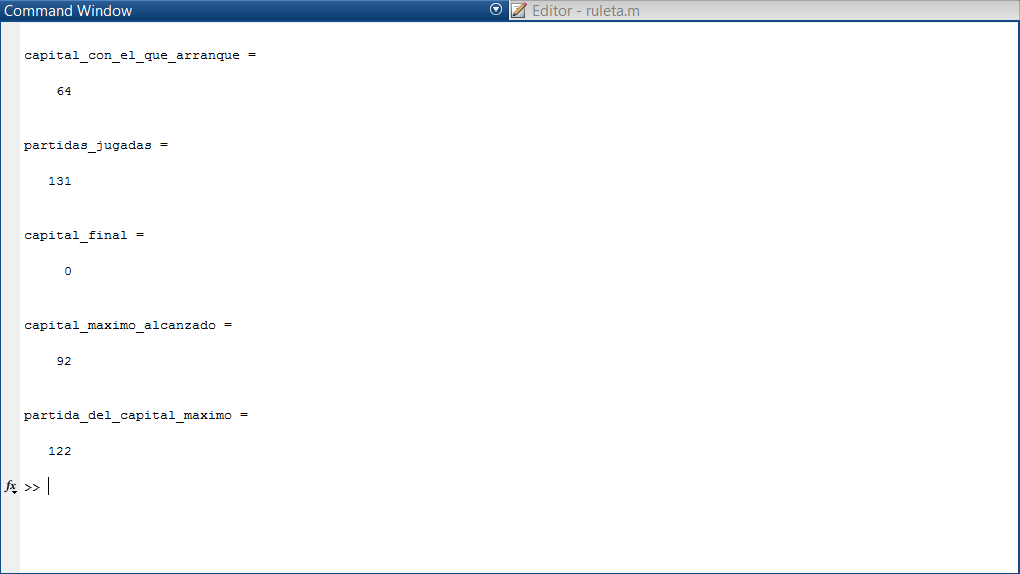
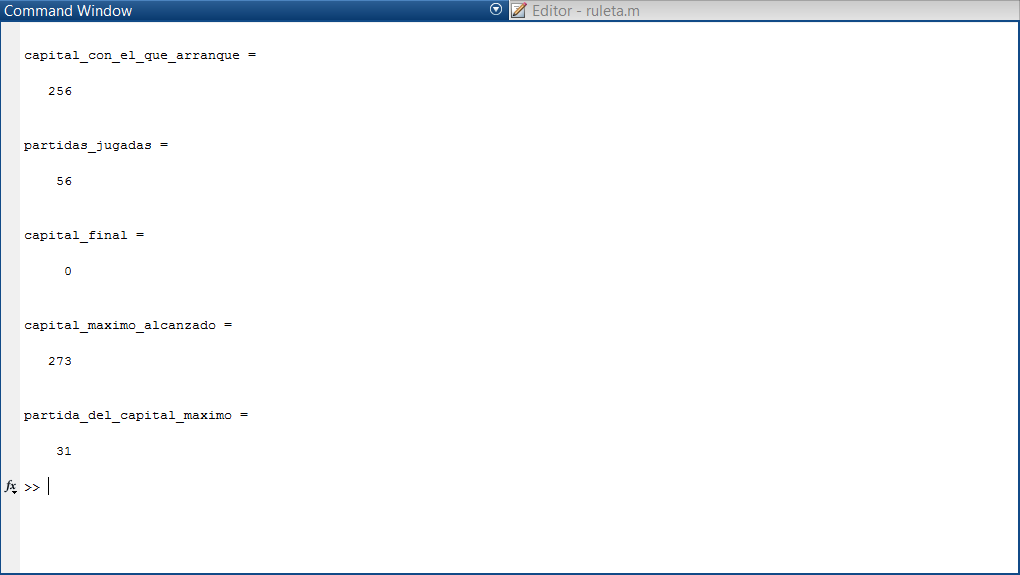
An interesting situation arises when studying the hypothetical case where the casino allows us to double a greater number of times (for the example, I take 20 times, which is 1,048,576 times the initial bet) and assuming we have the necessary money, we run the simulation for 1,000,000 days. It turns out that the probability of winning rises to 80%, but when analyzing the capital balance throughout the simulation, we find that we lost money. Despite winning 80% of the time, the capital needed to start each cycle that we lost was much greater than what was generated from the winning games.

Below, I leave images of some of the cycles (both positive and negative), the overall calculation for 1,000,000 days, and the hypothetical case.

In conclusion, I can assure you that you cannot win in a casino, no matter how good our technique is; in the long run, everything is designed to benefit the casino, so it should be avoided at all costs.

All games ultimately respond to the following equation:

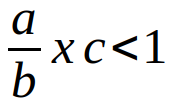
Where "a" represents the chances of winning, "b" represents all possible outcomes, and "c" is the payout received for winning that bet.

If the equation is less than 1 (and it always is in these cases), statistically, the game, in the long run, is benefiting the casino.

I leave you the link to download the MATLAB file if you are interested in examining it in greater detail.